Heat Conduction 3D

Heat Conduction 3D#

../../_images/heatconduction3d.png

Version

0

Design space

Box(0.0, 1.0, (51, 51, 51), float64)

Objectives

c: ↓

Conditions

volume: 0.3

area: 0.5

Dataset

IDEALLab/heat_conduction_3d_v0

Container

quay.io/dolfinadjoint/pyadjoint:master

Import

from engibench.problems.heatconduction3d.v0 import HeatConduction3D

HeatConduction 3D topology optimization problem.

Problem Description#

This problem simulates the performance of a Topology optimisation of heat conduction problems governed by the Poisson equation (https://github.com/dolfin-adjoint/pyadjoint/blob/master/examples/poisson-topology/poisson-topology.py)

Motivation#

Heat conduction problems serve as fundamental benchmarks for the development and evaluation of design optimization methods, with applications ranging from thermal management in electronic devices to insulation systems and heat exchangers in industrial applications. As thermal management has become critical in fields such as aerospace, automotive, and consumer electronics, both industry and academia have shown growing interest in advanced thermal design systems. In response to this demand, topology optimization has become popular as a powerful approach for improving heat dissipation while minimizing material usage. In addition, the development of additive manufacturing technologies has made the complex geometries produced by topology optimization more feasible to fabricate in real-world applications.

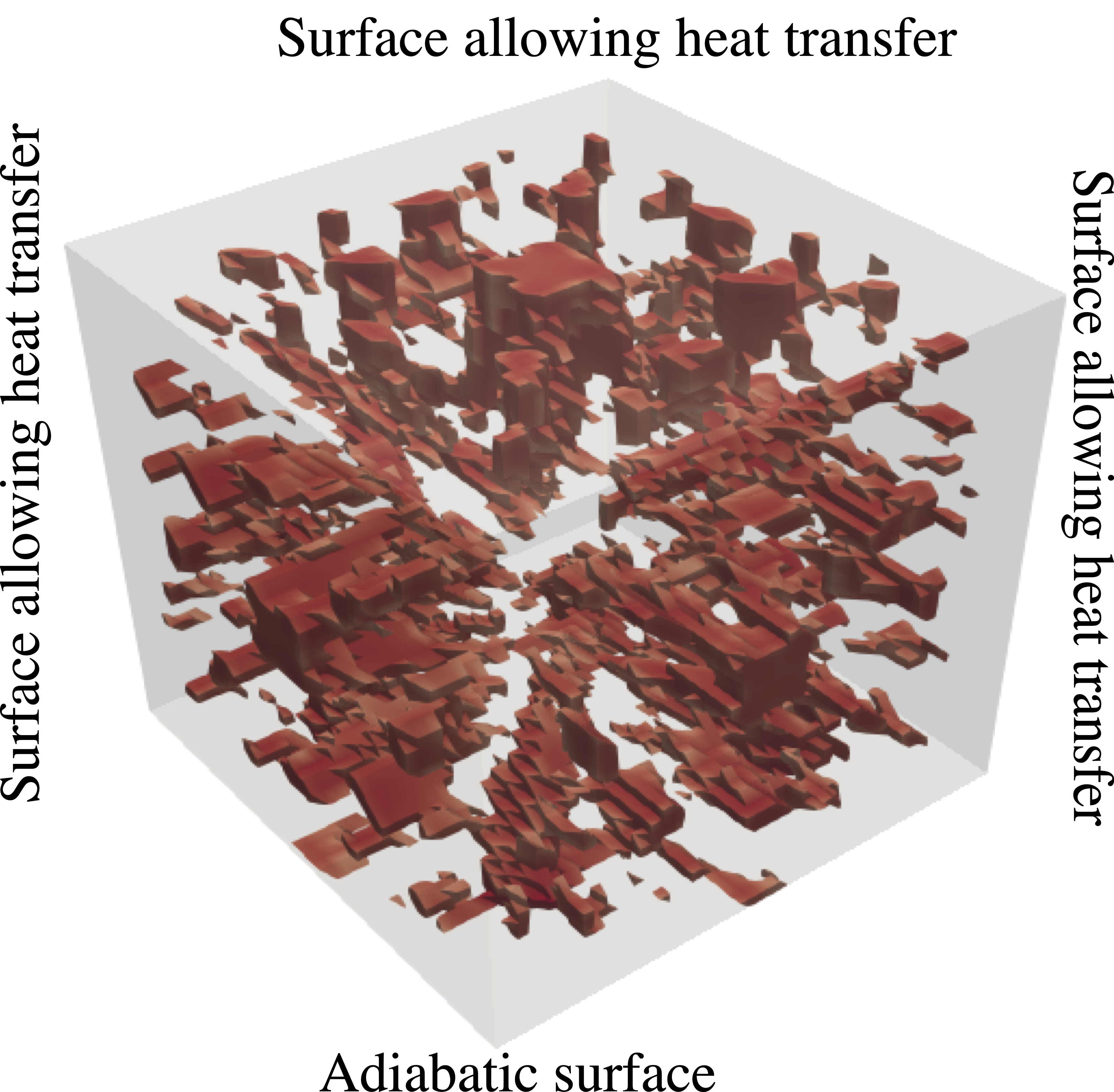
Design space#

These problems are a specific subset of topology optimization problems aimed at minimizing thermal compliance within a unit cube (3D), subject to: a constraint on the volume of highly conductive material used, and given boundary conditions, particularly the location of the adiabatic region. The adiabatic region refers to a prescribed symmetric area on the bottom surface of the 3D problem space. The 3D design space is represented as a 3D tensor of densities. By default, a \(51 \times 51 \times 51\) space is used for the 3D problem.

Objectives#

The objective is defined and indexed as follows:

  1. c: Thermal compliance coefficient to minimize.

Conditions#

The conditions are defined by the following parameters:

  • volume: the volume limits on the material distributions

  • area: The area of the adiabatic region on the bottom side of the design domain.

Simulator#

The simulator is a docker container with the dolfin-adjoint software that computes the thermal compliance of the design. We convert use intermediary files to convert from and to the simulator that is run from a Docker image.

Dataset#

The dataset has been generated the dolfin-adjoint software. It is hosted on the Hugging Face Datasets Hub.

v0#

Fields#

The dataset only contains conditions and optimal designs (no objective).

Creation Method#

The creation method for the dataset is specified in the reference paper.

References#

If you use this problem in your research, please cite the following paper: Habibi, Milad, Shai Bernard, Jun Wang, and Mark Fuge, “Mean squared error may lead you astray when optimizing your inverse design methods” in JMD 2025. doi: https://doi.org/10.1115/1.4066102

Lead#

Milad Habibi @MIladHB

Contents